선형연립방정식(system of linear equations)


이 모두 0일 경우를 동차선형연립방정식(homogeneous system of linear
equations, 동차선형방정식시스템)
일반적으로 선형연립방정식의 해가
존재하는 경우를 consistent라 하고 반면에 해가 존재하지 않는 경우를
inconsistent라 한다.
선형연립방정식의 해 전체의 집합을 선형연립방정식의 해집합(solution set)이라 하며, 동일한
해집합을 가지는 두 선형연립방정식을 동치(equivalent)라고 한다
주대각선성분(main diagonal entries)
n개의 미지수를 갖는 m개의 일차방정식으로 이루어진 선형연립방정식


계수행렬(coefficient matrix)

첨가행렬(augmented matrix)

선형연립방적식의 풀이 : 소거법 / GAUSS 소거법 / Gauss-Jordan 소거법




질문
REF와 RREF가 왜 정의되어야 하는지,
기본행 연산과 행동치가 왜 정의되어야 하는지,
행렬에 대하여 기본행 연산을 통해 REF와 RREF를 왜 구해야하는지.
Gauss 소거법: 선형연립방정식의 첨가행렬을 REF로 변형하여 푸는 방법이다.
Gauss-Jordan 소거법 : 선형연립방정식의 첨가행렬을 RREF로 변형하여 푸는 방법이다.

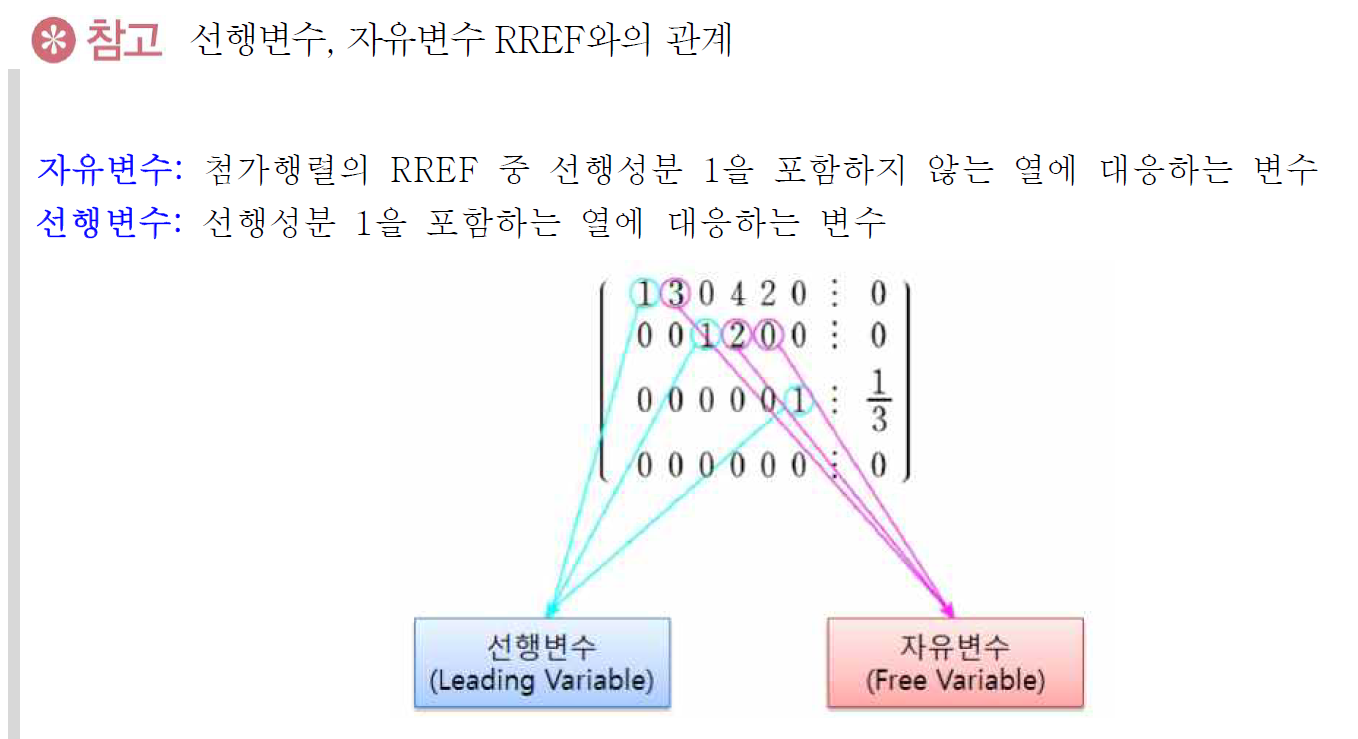
동차연립방정식은 (유일한) 자명한 해만을 갖는 경우와 무수히 많은 해를 갖는 두 가지 경우
밖에 없다.



n은 변수의 개수, m은 일차방정식의 개수
즉, 일차방정식의 개수가 변수의 개수보다 작으면 항상 자명하지 않은 해(x=0)를 갖는다.
'선형대수' 카테고리의 다른 글
| CH3. 행렬과 행렬대수 (2) (0) | 2022.11.18 |
|---|---|
| 선형대수 목차 (0) | 2022.11.18 |
| CH3. 행렬과 행렬대수 (1) (0) | 2022.11.18 |
| 선형대수 참고 사이트 (0) | 2022.11.16 |
| CH1. 벡터 (0) | 2022.11.15 |


