Upstage AI Lab 2기
2024년 1월 17일 (수) Day_026
Day_026 실시간 강의(1) : ML vs. Stats
Part1. 통계 톺아보기
(안창배 강사님)
통계학이 발달한 시점을 보면 19세기 말 ~ 20세기 초 -> 지금과 차이가 큼
(그 당시에는 분포표도 특허가 있었다?!)
왜도, 첨도 배우는 것도 이 시점부터 이어진 것, 오늘날은 왜도 첨도 계산해서 쓰는 일 잘 없음.
적률법 (Method of moments)
1차 평균, 2차 분산, 3차 왜도, 4차 첨도
(??? 자세한건 나중에 공부하기)
In statistics, the method of moments is a method of estimation of population parameters. The same principle is used to derive higher moments like skewness and kurtosis.
출처 : https://en.wikipedia.org/wiki/Method_of_moments_(statistics)

가정(Assumption)
- 통계적 모델에는 반드시 가정이 따름
- 정규성 - 잔차의 정규성!!!!
- 독립성
- 등분산성
정규성이 망가지면 등분산성이 망가지는 경우가 많고, 정규성을 고치면 등분산성도 고쳐지는 경우가 많음
정규성 (Normality)
QQplot(quantile–quantile plot)
log 변환하면 해결되는 경우도 많음

독립성 (Independency)
- 공간적 자기상관성
- 시간적 자기상관성
모델 자체에서 문제가 되는 경우는 많지 않음
regression 한 다음에 시계열 모델링(ARIMA,... 랑 뭐요?)으로 해결?
특성 활용과 모델은 다른 문제
등분산성 (Equal Variance)
2종 오류의 위험 증가
바틀렛 검정
mean이 커지면 분산도 커지는 것이 일반적 -> log 변환으로 skew를 잡아줌. ( + 수학적 증명 가능)
Welch t-test
assumption이 하나 사라짐
Log 변환의 효과
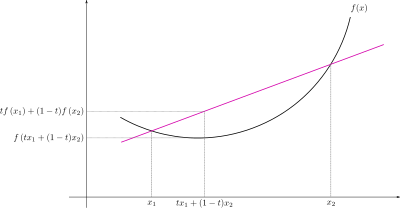
얀슨 Inequality (Jensen's inequality)
오차가 생기긴 하지만 크지 않다?

ANOVA의 결과로는 차이가 있음만 알 수 있을 뿐, 어느 부분에서 차이가 있는지는 알 수 없기 때문에 post-hoc 해야함
(가장 많이 쓰이는 것은 Tukey, 그 외에는 Bonferroni 정도)

Shingala, M. C., & Rajyaguru, A. (2015). Comparison of post hoc tests for unequal variance. International Journal of New Technologies in Science and Engineering, 2(5), 22-33.
통계적 유의미성 vs. 현실적 유의미성(regression과 R2)
통계의 regression : 선형회귀 모델
ML의 regression : classification에 대비되는 개념으로써 수치 예측하는 모델들
단순선형회귀 검증
Y = β0 + β1x + ε
귀무가설 : β1 != 0
β0 : bias
ε : 오차항
β1은 t 분포를 따르며 모델에 대한 검정은 F-분포를 이용
변수가 1개인 단순선형회귀의 경우 β1에 대한 t 검정은 F 검정으로 치환가능 (t^2=F 수리적으로 증명되어있음)
(t와 F 양측이라는 전제하에)

자유도 n-2 : β0 과 β1을 추정

단순선형회귀 평가
SST = SSE + SSR
(SSE - 모델이 예측하지 못하는 부분
SSR - 모델이 설명하는 부분)
R2 = SSR / SST = 1 - (SSE / SST)
(이론적 기반은 없음)


R2 과 p-value에 관한 썰
초봉과 휴학여부에 대한 상관관계를 분석하던 강사님의 학부동료들
p-value만 보면 유의미한데 R2 0.05왜 5%밖에 설명을 못하는지 모르겠다.교수님 : R2 0.05면 아주 훌륭하다. 관련있는 수많은 변수 중 5%면 훌륭하다.말하자면,
F-분포를 기반으로 한 p-value = 통계적 유의성
R2 = 현실적 설명력
p-value 대신 신뢰구간을 쓰자(from American Statistical Association)
https://www.amstat.org/asa/files/pdfs/p-valuestatement.pdf
https://amstat.tandfonline.com/doi/epdf/10.1080/00031305.2016.1154108?needAccess=true
Ron Kohavi
"Okay, if you're less than 0.05, but above 0.01, rerun, replicate."
So by lowering the P value, by forcing teams to work with the P value maybe below 0.01 and do replication on higher, then you can be much more successful, and the false positive rate will be much, much lower.
https://www.lennyspodcast.com/the-ultimate-guide-to-ab-testing-ronny-kohavi-airbnb-microsoft-amazon/
The ultimate guide to A/B testing | Ronny Kohavi (Airbnb, Microsoft, Amazon)
Brought to you by Mixpanel —Event analytics that everyone can trust, use, and afford | Round —The private network built by tech leaders for tech leaders …
www.lennyspodcast.com
요약 : p-value가 0.05~0.01이라면 데이터 수집을 더 해라
Adjusted R2
변수의 수가 늘어나면 무조건 R2 증가 ∴ 변수증가에 대한 패널티 필요
(이론적 기반은 없음)
'Upstage AI Lab 2기' 카테고리의 다른 글
| Upstage AI Lab 2기 [Day026] 실시간 강의 - 통계 (2) 머신러닝의 통계적 학습 (0) | 2024.01.18 |
|---|---|
| Upstage AI Lab 2기 [Day026] 온라인 강의 - 기초통계 (3) 실습 (0) | 2024.01.17 |
| Upstage AI Lab 2기 [Day026] 온라인 강의 - 기초통계 (2) (0) | 2024.01.17 |
| Upstage AI Lab 2기 [Day024] git-협업 (0) | 2024.01.15 |
| Upstage AI Lab 2기 [Day015-022] EDA 조별 프로젝트 (5) 설명변수 조합 (0) | 2024.01.09 |


