Upstage AI Lab 2기
2024년 1월 19일 (금) Day_028
Day_028 실시간 강의(2) :
(안창배 강사님)
왜 통계일까?
Average만 해도 다양한 방법이 있음
https://en.wikipedia.org/wiki/Average

예를 들어 poisson 분포의 경우 중앙값을 쓰면 안되고 절삭평균을 써야한다든지...
how to handle not stochastic issues?? 아니면 컴퓨터가 not stochastic?
Data Scientist -> Decision making
추정과 기댓값 (통계적 추론 Inference)
수치적 상관성
관계에 대한 가정이 있음. 이 가정이 만족되지 않으면 신뢰 X
통계는 굉장히 비직관적인 부분이 있는데 가설검정도 그런 부분 중 하나
신만이 모수를 알고 있다고 가정. 모수를 알수 없으니 표본으로부터 추정
모수(그리스문자로 표현) / 추정량(알파벳으로 표현) / 추정치 구분
추정량은 함수임
예를 들어 선형회귀에서 β^ 은 일반적으로 t 분포를 따름
계산하느니 증명한다는 stance. 오늘날은 증명하느니 계산한다는 stance.
전통적 통계학은 증명에 초점이 맞춰져 있음.
그러한 증명 중 하나가 추정량
추정량 (Estimator)
추정치 (Estimate)
추정량도 다양한 것이 있지만 그 중 MLE (Maximum Likelihood Estimator)
- unbiased - Log Transformation and Variance Stabilization
- efficient
- consistency
Bias-variance Tradeoff
Logarithmic transformation
https://optimization.cbe.cornell.edu/index.php?title=Logarithmic_transformation
Variance-stabilizing transformation
https://en.wikipedia.org/wiki/Variance-stabilizing_transformation
Gauss–Markov theorem
https://en.wikipedia.org/wiki/Gauss%E2%80%93Markov_theorem
- best linear unbiased estimator (BLUE)

미적/선형대수 필수
해석학 추천
선형대수 - 개념 정말 중요. Introduction to Linear Algebra - Gilbert strang (유투브 강의도 있음)
(주5시간 6개월이면 공부할 수 있을 듯)
칸아카데미?
1종 오류 / 2종 오류
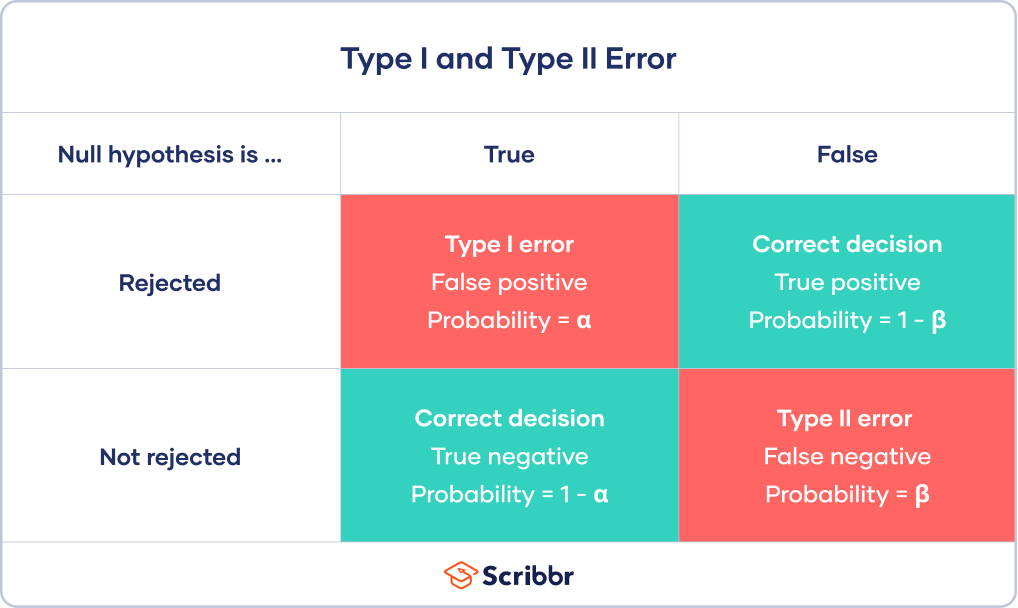
https://www.scribbr.com/statistics/type-i-and-type-ii-errors/
1종 오류 - 효과 없는데 있다고 나온 거
2종 오류 - 진실을 놓친거
현실에서도 1종 오류를 조금 더 중요하게 봄
Type I error를 고정(신뢰수준 95%, 99%)하고 Type II error 최소화
신뢰수준 Confidence Level
신뢰구간 Confidence Interval
주의! 모수는 고정된 숫자임. 확률이 존재할 수 없음
신뢰수준 ↑ 1종 오류 확률 ↓
통계는 연역적 학문임
이걸 거꾸로 본 게 bayesian
MLE (Maximum Likelihood Estimator)
Likelihood Function (가능도함수 / 우도함수)
https://en.wikipedia.org/wiki/Maximum_likelihood_estimation
L(θ ; x1, ... , xn) = f(x1, ..., xn ; θ)
=
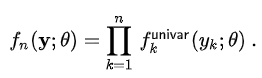
MLE, likelihood function, OLS 동치임을 증명할수 있음....
CLT도 변형이 몇가지 있고
몇가지 제약이 있음
iid 조건..
finite variance
outlier랑 왜도가 많이 해침, 왜도와 이상치 잡아주면 됨.
statistical learning
GLM - 변수와의 선형관계 -> link function
poisson 분포
- 단위시간 당 발생횟수 (공간당 발생횟수로 정의할 수도 있음)
예) 고객의 방문횟수, 음악 청취 횟수 등
but 너무 강한 제약 : 평균 / 분산이 같다. E(Y) = V(Y)
포아송 분포 정규/이항분포로 근사가 됨, 강한 제약때문에 한계가 있음.
통계 기반 ML : clustering
방법론이 잘 안 바뀌는 분야
통계적 가정을 잘 만지면 활용도 ↑
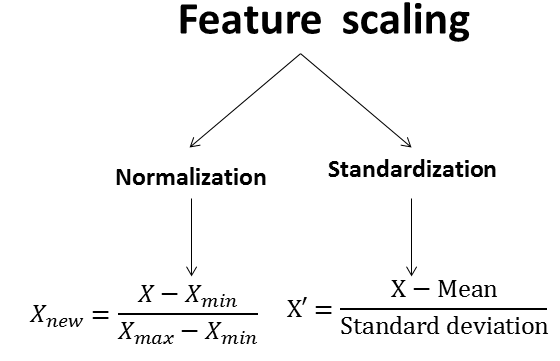
Normalization 0~1
Standardization (X-mu bar) / sigma
문제점 : 범주형 데이터를 dummy화할 때, 수치형 데이터와 범주형 데이터의 스케일을 같게 하는 것이 맞는가의 문제가 있을 수 있음
K-means
Nearest Neighbor 문제
수학적으로도 한번에 해결할 수 없음이 증명되어 있음
데이터의 분포가 찌그러지거나 군집간 수가 다르면 NG
K-medoids
Medoids are representative objects of a data set or a cluster within a data set whose sum of dissimilarities to all the objects in the cluster is minimal. Medoids are similar in concept to means or centroids, but medoids are always restricted to be members of the data set.
중앙값이란 다른 개념
추천쪽에서는 LDA로도 클러스터링을 할 수 있음
LDA(Latent Dirichlet allocation)
https://en.wikipedia.org/wiki/Latent_Dirichlet_allocation
Covariance
두 집단의 분산이 상관관계가 있다.
GMM (Gaussian Mixture Model)
Normal distribution = Gaussian distribution
but. 정규분포여야만 쓸 수 있는 것은 아님.
(정규분포는 outlier에 취약함)
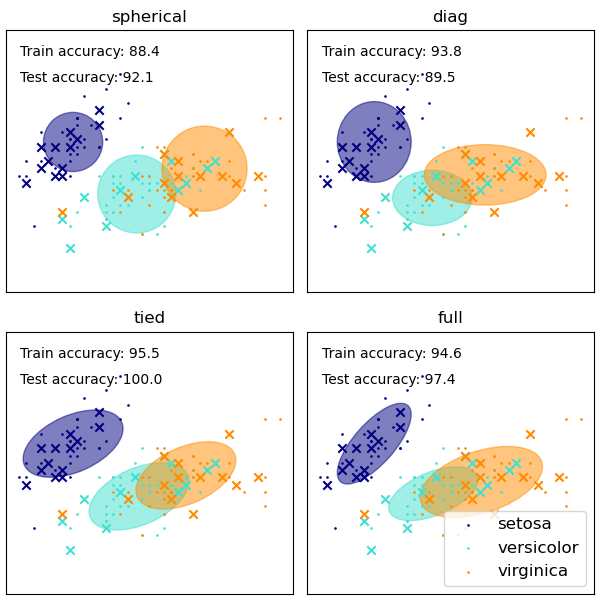
https://scikit-learn.org/stable/modules/mixture.html
https://scikit-learn.org/stable/auto_examples/mixture/plot_gmm_covariances.html
spherical - sphere, 군집 크기 다름
diag - 공분산 없음
Laplace Mixture Model
정규분포가 outlier에 취약한 것을 보완. outlier 제거.
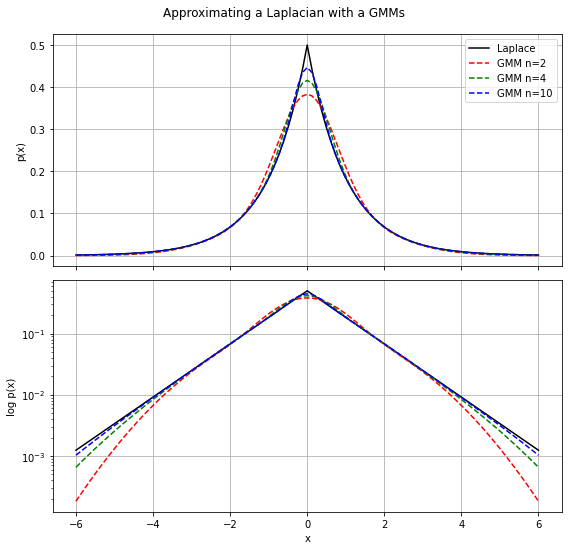
https://www.sitmo.com/gaussian-mixture-approximation-for-the-laplacian-distribution/
뭐가 제곱이 된다고요???
오늘의 K-means와 내일의 K-means가 달라짐.
K-means로 rule을 뽑아낸 뒤 rule 기반으로 fix 하는 방법을 쓰기도 함.
DBSCAN으로 이상탐지도 함.
모든 데이터를 포함시키진 않음
강사님 개인 의견 : 유클리드 거리 대신 likelihood function으로 내부로직을 바꿔볼 것 같음
행렬분해 -> 독립변수 압축
PCA / SVD
독립변수 너무 많으면 차원의 저주 문제
차원 ↑ 거리 ↑ -> 이웃이 없어짐. -> clustering 어렵고 noise ↑
PCA (Principal Component Analysis)
eigen value
note. iris data PCA 하기 좋음
손실이 최소화되도록 축 변환
한계 : 선형 상관관계만 압축할 수 있음
-> 그래서 DL에서는 autoencoder를 쓰기도

https://medium.com/analytics-vidhya/mathematics-behind-principal-component-analysis-pca-1cdff0a808a9
SVD (Singular Value Decomposition)
PCA와 SVD 연결되기는 함
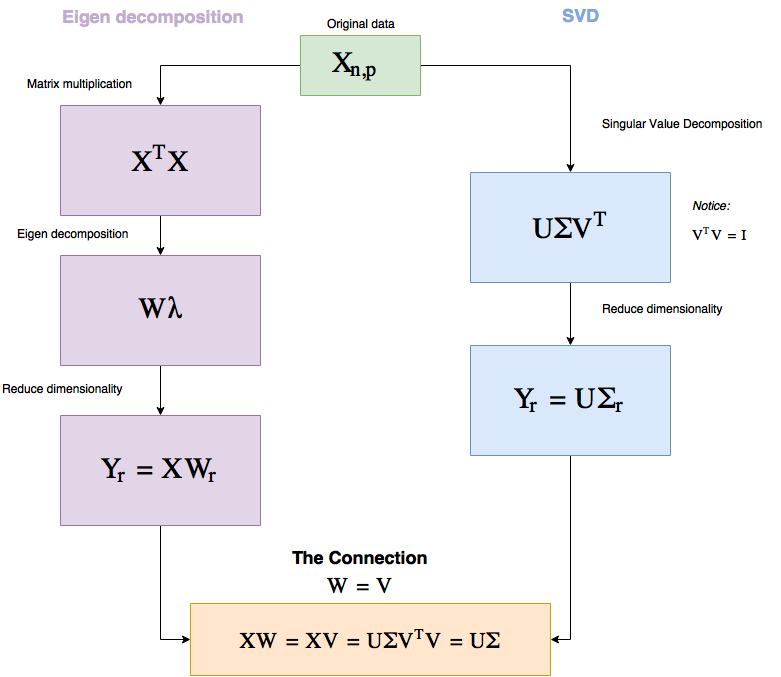

A = USVT가 두개의 행렬곱으로 표현 가능

https://medium.com/@kimminha1994/basics-of-recommendation-system-f01c499e2550
데이터 조금 변형됨
차원 축소 후 다시 확장
embedding matrix를 생성
SVD의 한계와 ALS(Alternative Least Square)
-> sparsity 문제
-> PCA와 SVD 시간복잡도 ↑
sparse matrix를 만들면 1% 미만으로 보존 가능 (row, column, value)
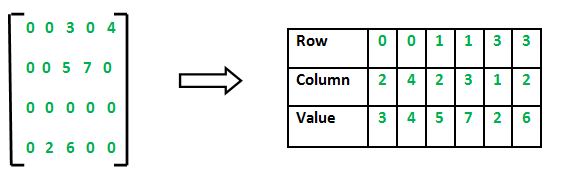
https://medium.com/@sudeesh335/what-is-spare-matrix-d4448f27490f
ALS(Alternative Least Square)
초심자는 ALS 이기는 모델 만들기 어려움
(10년 넘은 모델)
U 와 V를 번갈아 학습
Matrix Factorization
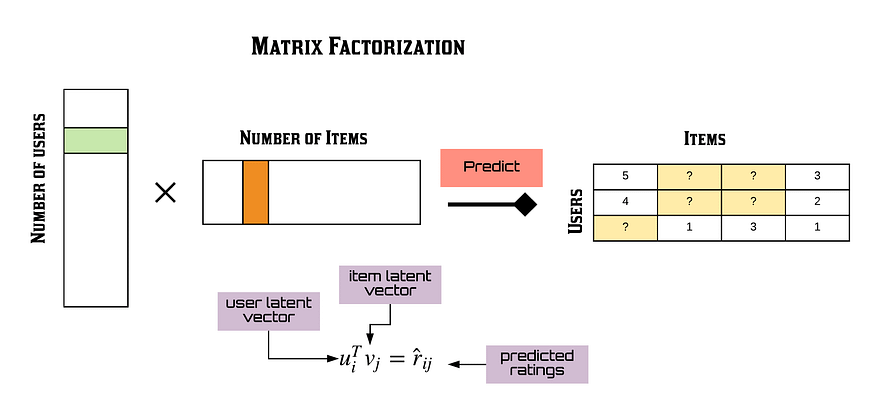
Annoy - Spotify
hashing algorithm
faiss, annoy, n2 정도

https://github.com/spotify/annoy
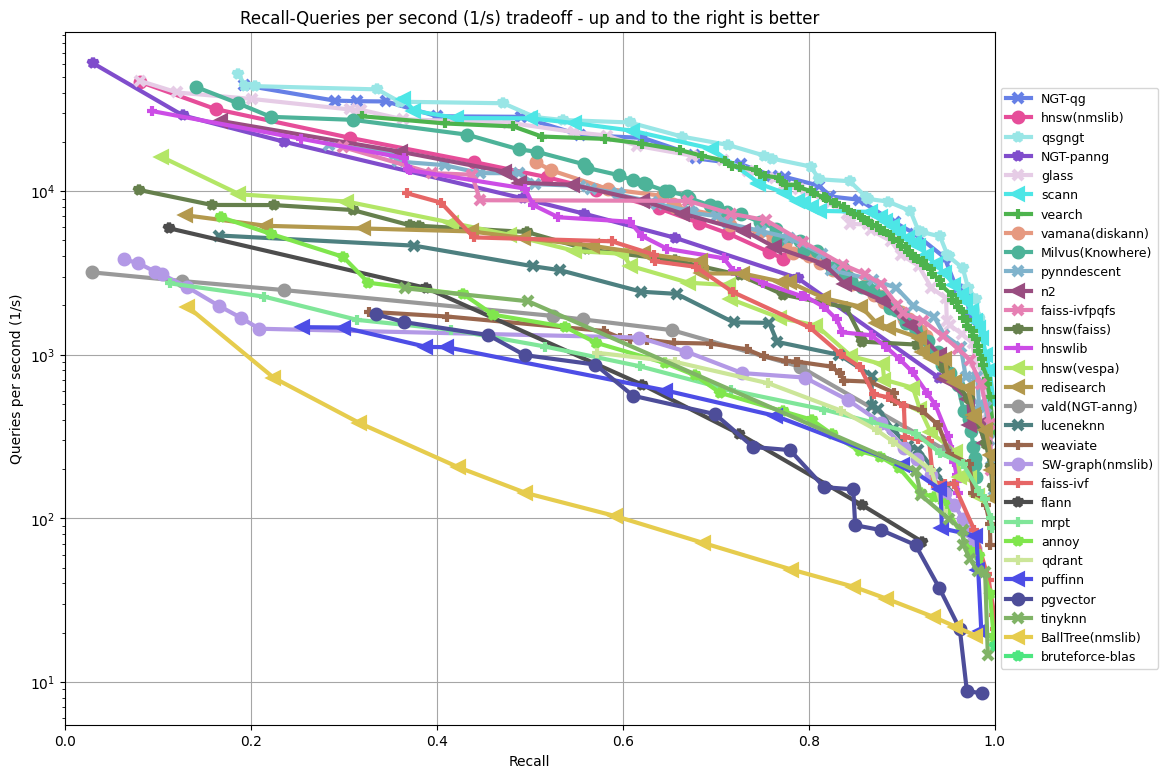
실습 코드
추천 패키지
implicit, surprise, buffalo
sparse matrix로 고쳐서 ALS
(sparse matrix : 빈 칸을 버린 matrix / row, column, value로 변환한 matrix)
패키지마다 가공방식 다르니 주의
그러면 그룹별 매출이 다른지 어떻게 아는가 -> ANOVA
K-means는 다중공선성 고려 x
GMM 해보면 됨
ANOVA -> 잔차에 대해!! residual!!
GMM 자체가 equal variance를 전제하지 않음
정량적 접근 뿐만 아니라 정성적 접근도 필요. 특히 초보자는 실수할 가능성이 많기 때문에 생각하는 흐름과 잘 맞는지 체크하면서.
join은 엄청 무거운 연산
한줄로 넣을수 있으면 연산 측면에서 이점이 큼
about fat pandas
뚱뚱하고 굼뜬 판다(Pandas)를 위한 효과적인 다이어트 전략
https://www.youtube.com/watch?v=0Vm9Yi_ig58
https://drive.google.com/file/d/12faqaslFIF-Sg_sU3jeGyauW5ClRqS8D/view
'Upstage AI Lab 2기' 카테고리의 다른 글
| Upstage AI Lab 2기 [Day031] Machine Learning Workflow (1) (0) | 2024.01.24 |
|---|---|
| Upstage AI Lab 2기 [Day031] 머신러닝 기초 개념 이해 (1) (0) | 2024.01.23 |
| Upstage AI Lab 2기 [Day026] 실시간 강의 - 통계 (3) Statistical Learning (0) | 2024.01.18 |
| Upstage AI Lab 2기 [Day027] 선형회귀분석 (0) | 2024.01.18 |
| Upstage AI Lab 2기 [Day026] 실시간 강의 - 통계 (2) 머신러닝의 통계적 학습 (0) | 2024.01.18 |



